西安电子科技大学计算方法期末5

考试时间：90分钟
一. 填空（每空3分，共15分）
1. 的精确值为3.1415926......，取的近似值x₁ = 3.142，则x₁有     位有效数字；取的近似值x₂ = 3.141，则x₂有      位有效数字。     


2. 在区间[0, 2]上的插值型求积公式系数为＝
         。

 
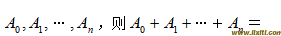3. 设ƒ(x)= lnx，取x₁= 0，x₂= 0.5，x₃=1.5，x₄=3，x₅=4，在这些点上关于ƒ(x)的牛顿插值多项式为L₄(x)，则ƒ(1.5) – L₄(1.5) =        。

 
4．已知函数y = f (x)在点x₁、x₂和x₃处的函数值为f(x₁)=10 、f(x₂)=15和f(x₃)=13，用插值型求导公式的三点公式计算得        。

 
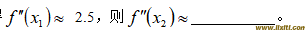二.选择 （每空3分，共15分）
1．设ƒ(x)= sinx，取x₁ = 0.32，x₂ = 0.34，x₃ = 0.36，x₄ = 0.38，x₅ = 0.40，用四次拉格朗日插值公式计算0.39处的近似函数值为L₄f (0.39)，计算时间为T_L；用四次牛顿插值公式计算0.39处的近似函数值为N₄f (0.39)，计算时间为T_N。从理论上分析，如果用相同的计算机计算，有下列结论成立：（1）            ；（2）           。
（1）A.  L₄= N₄          B.  L₄N₄
（2）A.  T_L < T_N         B.  T_L = T_N           C. T_L > T_N

 
2．通过          个点来构造多项式的插值问题称为抛物线插值。
A. 2          B. 3         C. 4      

 
3. 以下方程求根的数值计算方法中，收敛速度最快的是       ，收敛速度最慢的是
        。
A. 简单迭代法   B.二分法    C. 牛顿迭代法    D. 割线法

 
三. 用牛顿法求解非线性方程x(x+1)² -1=0在x = 0.4附近的根,保留五位有效数字。（10分）

 
四.已知函数f (x)的数值表：（15分）

 
（1） 求各阶向前差分；
（2） 写出向前牛顿插值公式N₃(x)；
（3） 计算f (4)的近似值。

 
五. 用数值法求解定积分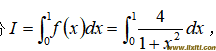，已知精确值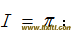：（15分）
   （1）取h = 1/8，用复化梯形公式计算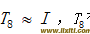有几位有效数字？
   （2）取h = 1/4，用复化辛普生公式计算，有几位有效数字？
 

 
六. 用数值法求解线性方程组：（15分）
    
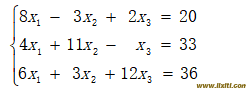
（1） 写出雅可比迭代公式、雅可比迭代矩阵，判断雅可比迭代法是否收敛；
（2） 写出高斯-赛德尔迭代公式、高斯-赛德尔迭代矩阵，判断高斯-赛德尔迭代法是
 否收敛；
（3） 若雅可比迭代法和高斯-赛德尔迭代法均收敛，哪种方法收敛更快？为什么？

 
七. 用四阶龙格-库塔公式法解微分方程：（15分）